6.1 ECES ~ Key Agreement Recall that the Elliptic Curve Discrete Logarithm Problem is basically defined as: Given a P and Q over an elliptic curve group, find k such that kP = Q. When applied in a public-key cryptosystem, k is the private key, and Q becomes the public key. Even though Q is called the public key, Q by itself does not control encryption. Instead, Q in combination with one more number, creates the true secret value in which with the encryption is produced. This secret value (z), is a one-time shared number that is generated through a key agreement scheme. Through a key agreement scheme, a secret value may be exchanged without any outside observers being able to determine what it is. 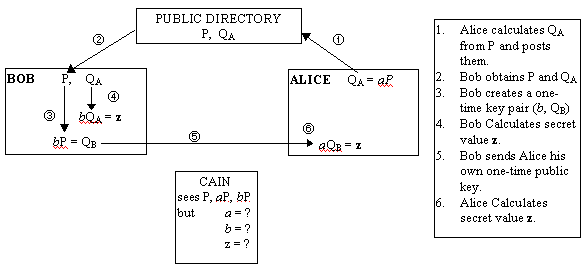For example, take the scenario of Alice and Bob who wish to communicate securely. In this case, Bob wishes to send Alice a message. With Alice's private key a, she computes her public key QA (where QA = aP) and posts it on a public directory along with P. Meanwhile Bob creates a one-time key pair by selecting a random integer b. This key will only be used once for this particular transmission. Bob then proceeds to perform two calculations: He determines his one-time public key QB where QB = bP and determines the secret value z, where z = bQA. Bob now has the secret value which he computed through the scalar multiplication of Alice's public key by b. Next, Bob must let Alice know the value of z, without telling her directly what it is. He does this by sending Alice his own one-time public key, QB. Alice now calculates z through the calculation: z = aQB. This works since z = b(aP) = a(bP).
.	Certicom is a trademark of the Certicom Corp. © Copyright Certicom Corp. 1997. All rights reserved. Comments or Questions about this site? Please contact info@certicom.ca