2.1 Elliptic Curve Arithmetic: A Geometric Approach Elliptic curve groups are additive groups; that is, their basic function is addition. The addition of two points in an elliptic curve is defined geometrically. The negative of a point P = (xP,yP) is its reflection in the x-axis: the point -P is (xP,-yP). Notice that for each point P on an elliptic curve, the point -P is also on the curve. 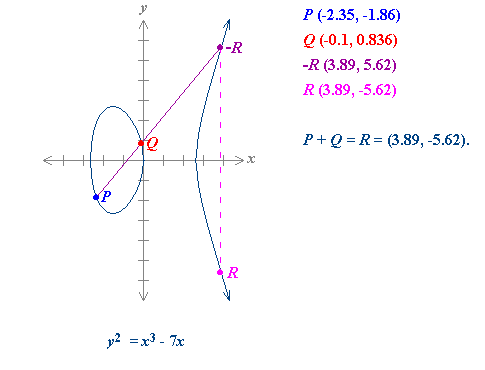2.1.1 Adding distinct points P and Q Suppose that P and Q are two distinct points on an elliptic curve, and the P is not -Q. To add the points P and Q, a line is drawn through the two points. This line will intersect the elliptic curve in exactly one more point, call -R. The point -R is reflected in the x-axis to the point R. The law for addition in an elliptic curve group is P + Q = R. For example:
P + Q = R is the additive property defined geometrically.
	Certicom is a trademark of the Certicom Corp. © Copyright Certicom Corp. 1997. All rights reserved. Comments or Questions about this site? Please contact info@certicom.ca