2.0 Elliptic Curve Groups over Real Numbers An elliptic curve over real numbers may be defined as the set of points (x,y) which satisfy an elliptic curve equation of the form: y2 = x3 + ax + b, where x, y, a and b are real numbers. Each choice of the numbers a and b yields a different elliptic curve. For example, a = -4 and b = 0.67 gives the elliptic curve with equation y2 = x3 - 4x + 0.67; the graph of this curve is shown below:
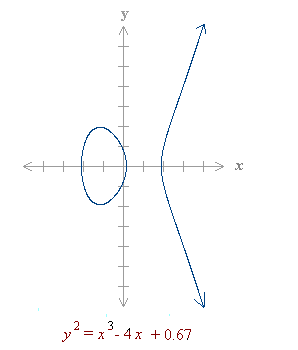
There are infinitely many points on such an elliptic curve. There are infinitely many points on such an elliptic curve.		If x3 + ax + b contains no repeated factors, or equivalently if 4a3 + 27b2 is not 0, then the elliptic curve y2 = x3 + ax + b can be used to form a group. An elliptic curve group over real numbers consists of the points on the corresponding elliptic curve, together with a special point O called the point at infinity.
	Certicom is a trademark of the Certicom Corp. © Copyright Certicom Corp. 1997. All rights reserved. Comments or Questions about this site? Please contact info@certicom.ca