Elliptic Curve Classroom (JAVA required) 6.5 ECES ~ A Simple Example



System Setup:

The underlying finite field will be F24 and the elliptic curve is described by the following equation: E = y2 + xy = x3 + g3 (here: a = 0, b = g3)

The point P = (xP, yP) = (g5, g11) is selected. Since 5P = O, the point P has the order n = 5. The public information (system parameters) are the field of F24, the curve E, the point P, and the order n = 5.

Key Generation (done prior to ECES)

Party A performs the following operations:

  1. A selects a random integer d = 3 in the interval [2, n-2] = [2,3]
  2. A computes the point Q = dP = 3(g5,g11) = (g,0) = ((1100),(0000))
  3. A makes public the point Q.
  4. A's private key is the integer d.

Encryption Process

Party B performs the following steps in order to send the message M = 010100 to Party A:

  1. B looks up A's public key: Q = (xQ, yQ) = (g,0).
  2. B selects a random integer k = 2 in the interval [n, n-2] = [2,3] - the private key for the one-time key pair.
  3. B computes the point (x1,y1) = kP = 2(g5,g11) = (g,g) = ((1100),(1100)) - the public key for the one-time key pair.
  4. B computes the point (x2,y2) = kQ = 2(g,0) = (g5,g11) = ((1010),(1110)). x2 is the secret value.
  5. B generates a mask Y of length 6 with the mask generation function from the secret value x2. Depending of the mask generation function used, Y will vary. For the purposes of this example, let Y = 011010.
  6. B computes C = Y 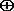M = (011010) 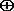(010100) = (001110)
  7. B computes the encrypted message by concatenating (x1,y1) and C and transmits (11001100001110) to Party A

Decryption Process

Party A performs the following steps in order to decrypt the ciphertext EM = 11001100001110 received from B.

  1. A uses the first 8 bits of the string for the one-time public key: ((1100),(1100)). The rest of EM will be stored in C.
  2. A computes the point (x2,y2) = d(x1,y1) = 3(1100,1100) = 3(g,g) = (g5,g11) = ((1010),(1110)). x2 is the secret value.
  3. Using the same mask generation function as B, A generates from x2 the mask Y = 011010.
  4. A recovers the message M by XORing all but the first 8 bits of EM with the mask Y: M = C 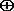Y = (001110) 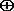(011010) = (010100)

[back][previous menu][next].


Certicom is a trademark of the Certicom Corp. © Copyright Certicom Corp. 1997. All rights reserved.

Comments or Questions about this site? Please contact info@certicom.ca