An Example of an EC group over F2m

4.1 An Example of an Elliptic Curve Group over F₂m

As a very small example, consider the field F₂4, defined by using polynomial representation with the irreducible polynomial f(x) = x⁴ + x + 1. The element g = (0010) is a generator for the field . The powers of g are:
g⁰ = (0001) g¹ = (0010) g² = (0100) g³ = (1000) g⁴ = (0011) g⁵ = (0110)
g⁶ = (1100) g⁷ = (1011) g⁸ = (0101) g⁹ = (1010) g¹⁰ = (0111) g¹¹ = (1110)
g¹² = (1111) g¹³ = (1101) g¹⁴ = (1001) g¹⁵ = (0001)
In a true cryptographic application, the parameter m must be large enough to preclude the efficient generation of such a table otherwise the cryptosystem can be broken. In practice, m = 155 would be a suitable choice. The table allows the use of generator notation (g^e) rather than bit string notation, as used in the following example. Also, using generator notation allows multiplication without reference to the irreducible polynomial (f(x) = x4 + x + 1).

Note:
Addition with bit-strings is controlled by an XOR function.
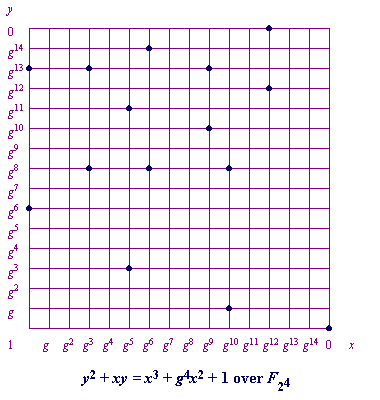
Consider the elliptic curve y² +xy = x³ + g⁴x² + 1. Here a = g⁴ and b = g⁰ =1. The point (g⁵, g³) satisfies this equation over F₂m:
y² + xy = x³ + g⁴x² + 1
(g³)² + g⁵g³ = (g⁵)³ + g⁴g¹⁰ + 1
g⁶ + g⁸ = g¹⁵+ g¹⁴+ 1
(1100) + (0101) = (0001) + (1001) + (0001)
(1001) = (1001)
The fifteen points which satisfy this equation are:
(1, g¹³) (g³, g¹³) (g⁵, g¹¹) (g⁶, g¹⁴) (g⁹, g¹³) (g¹⁰, g⁸) (g¹², g¹²)
(1, g⁶) (g³, g⁸) (g⁵, g³) (g⁶, g⁸) (g⁹, g¹⁰) (g¹⁰, g) (g¹², 0) (0, 1)
These points are graphed below:

Certicom is a trademark of the Certicom Corp. © Copyright Certicom Corp. 1997. All rights reserved.

Comments or Questions about this site? Please contact info@certicom.ca