3.1 Example of an Elliptic Curve Group over Fp As a very small example, consider an elliptic curve over the field F23. With a = 1 and b = 0, the elliptic curve equation is y2 = x3 +x. The point (9,5) satisfies this equation since: y2 mod p = x3 + x mod p 52 mod 23 = 93 + 9 mod 23 25 mod 23 = 738 mod 23 2 =2
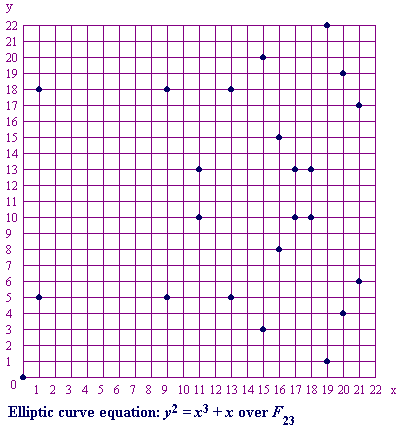
Note the seemingly random spread of points for the elliptic curve over Fp.	The 23 points which satisfy this equation are: (0,0) (1,5) (1,18) (9,5) (9,18) (11,10) (11,13) (13,5) (13,18) (15,3) (15,20) (16,8) (16,15) (17,10) (17,13) (18,10) (18,13) (19,1) (19,22) (20,4) (20,19) (21,6) (21,17) These points may be graphed as below: Note that there is two points for every x value. Even though the graph seems random, there is still symmetry about y = 0.5p
	Certicom is a trademark of the Certicom Corp. © Copyright Certicom Corp. 1997. All rights reserved. Comments or Questions about this site? Please contact info@certicom.ca