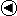F24 with Optimal Normal Basis Representation
The elements of F24 are all binary strings of length 4. Addition and subtraction are defined as with polynomial representation.
Setup for Multiplication
- The field F24 has a Type I Optimal Normal Basis; thus f(x) = x4 + x3 + x2 + x + 1. The set of polynomials {x, x2, x4, x8} forms a normal basis of F24 over F2.
The rows of A are constructed as follows:
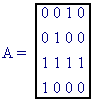
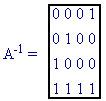
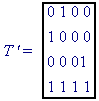
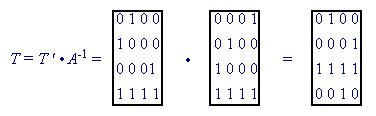
l0,0 = T(0,0) = 0 l1,0 =T(3,3) = 0 l2,0 = T(2,2) = 1 l3,0 = T(1,1) = 0
l0,1 = T(1,0) = 0 l1,1 =T(0,3) = 0 l2,1 = T(3,2) = 1 l3,1 = T(2,1) = 1
l0,2 = T(2,0) = 1 l1,2 =T(1,3) = 1 l2,2 = T(0,2) = 0 l3,2 = T(3,1) = 0
l0,3 = T(3,0) = 0 l1,3 =T(2,3) = 1 l2,3 = T(1,2) = 0 l3,3 = T(0,1) = 1
Multiplication
Multiplication is defined by (a0 a1 a2 a3) (b0 b1 b2 b3) = (c0 c1 c2 c3), where
c0 = a0b2 + a1(b2 + b3) + a2(b0 + b1) + a3(b1 + b3)
c1 = a1b3 + a2(b3 + b0) + a3(b1 + b2) + a0(b2 + b0)
c2 = a2b0 + a3(b0 + b1) + a0(b2 + b3) + a1(b3 + b1)
c3 = a3b1 + a0(b1 + b2) + a1(b3 + b0) + a2(b0 + b2).
Thus (0 1 0 0) (1 1 0 1) = (c0 c1 c2 c3), where
c0 = 0(0) + 1(0 + 1) + 0(1 + 1) + 0(1 + 1) = 1
c1 = 1(1) + 0(1 + 1) + 0(1 + 0) + 0(0 + 1) = 1
c2 = 0(1) + 0(1 + 1) + 0(0 + 1) + 1(1 + 1) = 0
c3 = 0(1) + 0(1 + 0) + 1(1 + 1) + 0(1 + 0) = 0,
and (0 1 0 0) (1 1 0 1) = (1 1 0 0).
Exponentiation using Optimal Normal Bases
The squaring (a0 a1 a2 a3)2 = (a0 a1 a2 a3) (a0 a1 a2 a3) = (c0 c1 c2 c3), where
c0 = a0a2 + a1(a2 + a3) + a2(a0 + a1) + a3(a1 + a3) = a32 = a3
c1 = a1a3 + a2(a3 + a0) + a3(a1 + a2) + a0(a2 + a0) = a02 = a0
c2 = a2a0 + a3(a0 + a1) + a0(a2 + a3) + a1(a3 + a1) = a12 = a1
c3 = a3a1 + a0(a1 + a2) + a1(a3 + a0) + a2(a0 + a2) = a22 = a2.
Thus (a0 a1 a2 a3)2 = (a3 a0 a1 a2) can be calculated with a simple rotation of (a0 a1 a2 a3). Squaring is a very efficient operation when optimal normal basis representation is used. Since exponentiation typically involves many squaring operations, exponentiation is performed far more efficiently using optimal normal basis representation than using polynomial representation.