 Hint for the
Mercedes Knot Problem:
Hint for the
Mercedes Knot Problem:
 Hint for the
Mercedes Knot Problem:
Hint for the
Mercedes Knot Problem:
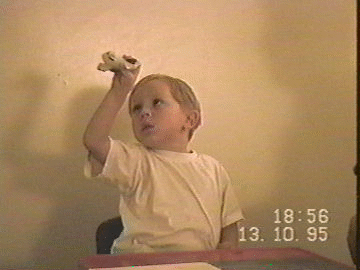
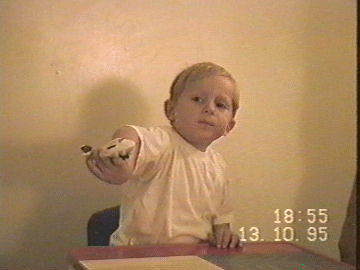
Let us use our imagination (if not some childhood memories) and picture a boy or a girl sitting at the desk, trying to satisfy the parents by studying some thick boring book. The child soon gets tired and starts to play with a plastic model of an airplane. The plane has to fly forward on and on (planes do not fly backwards, remember?), while being hold firmly in one hand, however it would not be wise to move from the chair (the floor is squeaky and the parents might realize that their kid is not studying any more), and the plane cannot be turned upside down. The child pretends to be a pilot of a commercial plane and passengers would get angry if the pilot did otherwise, at least those who do not use their seat-belts. Suddenly the child finds out that the plane can be moved along a path that has the shape of number 8. "Amazing", the kid thinks, "if I moved the plane along a path in the shape of a circle my hand would tangle, and I would have to stop, but 8 works".
Could we use this ingenious solution in our problem? Well, let us twist and fold this figure of eight so that we see from the top only one "circle" (a mathematician would say that such an eight covers a circle, see Figure 2).
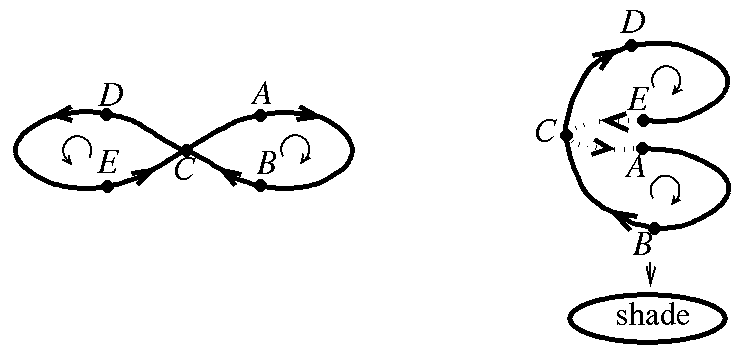
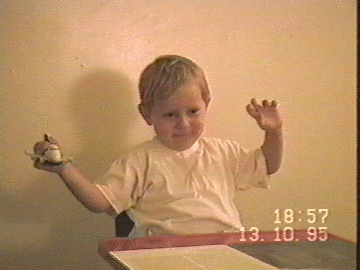
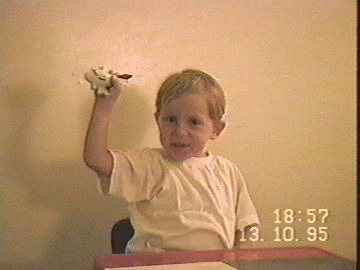
The child has still no problem flying the plane in the path of this folded eight shape. Try it yourself; Figure 3 might be helpful (similar pictures have appeared in many journals and books). But the child is now moving the plane in the path of a circle (for that reason we fold 8 completely), with the arm returning to the same position only after two full circles (during the first circle the elbow goes above the plane, while during the second circle it stays below the plane). There is no problem in making these circles so small that the plane is eventually just rotating. So the child can rotate the plane in the same direction constantly while holding it firmly in the hand . Actually, we can even say that we can rotate our hand constantly in the same direction while it is turned up all the time.
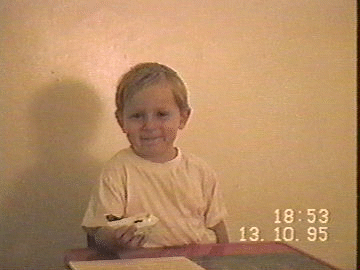

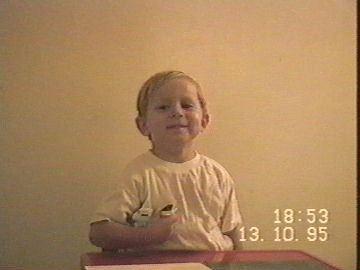
 Aleksandar Jurisic, ajurisic@valjhun.fmf.uni-lj.si, December 1996.
Aleksandar Jurisic, ajurisic@valjhun.fmf.uni-lj.si, December 1996.