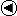F24 with Polynomial Representation
The elements of F24 are the 16 vectors:
The irreducible polynomial used will be f(x) = x4 + x + 1. The following are sample calculations.
Addition
(0110) + (0101) = (0011).
Multiplication
(1101) (1001)
= (x3 + x2 + 1) (x3 + 1) mod f(x)
= x6 + x5 + 2x3 + x2 + 1 mod f(x)
= x6 + x5 + x2 + 1 mod f(x) (coefficients are reduced modulo 2)
= ( x4 + x + 1)(x2 + x) + (x3 + x2 + x + 1) mod f(x)
= x3 + x2 + x + 1
= (1111).
Exponentiation
To compute (0010)5, first find
(0010)2
= (0010) (0010)
= x x mod f(x)
= ( x4 + x + 1)(0) + (x2) mod f(x)
= x2
= (0100).
Then
(0010)4
= (0010)2 (0010)2
= (0100) (0100)
= x2 x2 mod f(x)
= ( x4 + x + 1)(1) + (x + 1) mod f(x)
= x + 1
= (0011).
Finally, (0010)5
= (0010)4 (0010)
= (0011) (0010)
= (x + 1) (x) mod f(x)
= (x2 + x) mod f(x)
= ( x4 + x + 1)(0) + (x2 + x) mod f(x)
= x2 + x
= (0110).
Multiplicative Inversion
The element g = (0010) is a generator for the field. The powers of g are:
The multiplicative identity for the field is g0 = (0001). The multiplicative inverse of g7 = (1011) is g-7 mod 15 = g8 mod 15 = (0101). To verify this, see that
(1011) (0101)
= (x3 + x + 1) (x2 + 1) mod f(x)
= x5 + x2 + x + 1 mod f(x)
= ( x4 + x + 1)(x) + (1) mod f(x)
= 1
= (0001),
which is the multiplicative identity.