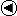The field Fp
The finite field Fp (p a prime number) consists of the numbers from 0 to p - 1. Its operations are addition and multiplication, which are defined as for the groups Zn and Zp* respectively: all calculations end with reduction modulo p. The restriction that p be a prime number is necessary so that all non-zero elements have a multiplicative inverse (see Zp* for details). As with Zn and Zp*, other operations in Fp (such as division, subtraction and exponentiation) are derived from the definitions of addition and multiplication.
Calculations in the field F23 include
10 4 - 11 mod 23
= 29 mod 23
= 6
7-1 mod 23
= 10
since
7 10 mod 23
= 70 mod 23
= 1
(83) / 7 mod 23
= 512 / 7 mod 23
= 6 7-1 mod 23
= 6 10 mod 23
= 14.
Certicom is a trademark of the Certicom Corp. Copyright Certicom Corp. 1997. All rights reserved.